前回のエントリーで紹介した本が読み終わったので(後半、数理計画問題とか知らなかったから読むのつらかったー。とりあえず近似解方のあたりが特に知りたかったので後半は斜め読み(;´Д`))、とりあえず自分に関係ありそうなところだけまとめておく。
:近似解法
nearest neighbor method
とりあえず最も近い拠点からどんどん繋げていきましょうと言う古典的な方法。途中まではイイ感じに進むが、最後ら辺でコスト大な経路が発生する。
:改善法
2-opt,3-opt
経路をいくつか(2or3本)選んで繋ぎ変える。
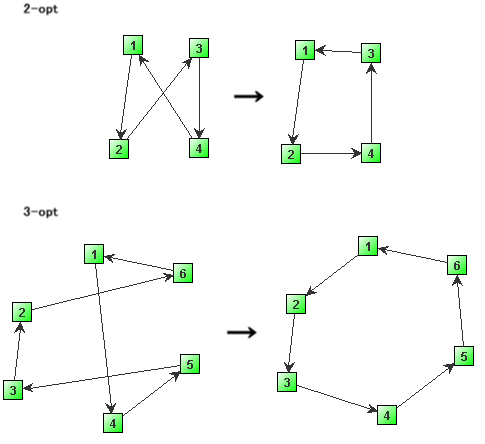
もし繋ぎ変えた結果、全体の経路が短くなってればそれ採用。
が、図を書いて気づいたのだが、繋ぎ変えてない箇所の順路の向きが変わる場合があるのね。図の2-optの例で言うと3→4だったのが繋ぎ変えた後だと4→3になる。
ちなみにもっと繋ぎ変える本数を大きくしたのをλ-optと言うらしい。が、3より大きくなると繋ぎ変えるパターンを把握するのが大変なのでプログラミングしづらい。なので実用的な範囲は2~3らしい。
ちなみにλを動的に変化させる手法もあり(LinとKernighanの算法)、こちらは改善する前の巡回路の影響を受けにくい性質を持つため、よく使われる。(これをベースとして改良した様々な手法が出てるがこれは後々調べることにする。)
---
んでさっきのnearest neighbor methodの話に戻るけど、この手法で求められた巡回路は最適巡回路と多くの枝を共有していると言われているので改善法と組み合わせれば最後の詰めで発生したコスト大な経路が無くなり、ナイスな答えになる。
個人的に知りたかったnearest insertion methodについての話がなかったのが残念(´・ω・`)
とりあえずそろそろプログラムの方に取りかかることにしよう。
